Subiectele de la Evaluarea Națională, rezolvate de un profesor de matematică din Sibiu. „Calculele, mai ales pe partea de geometrie, nu au fost cele mai simple”

Elevii sibieni au susținut miercuri, 25 iunie, examenul scris la matematică în cadrul Evaluării Naționale 2025. Cu ajutorul unui profesor de matematică din Sibiu mai jos se poate consulta modul de rezolvare al exercițiilor.

Potrivit profesorului, subiectele, mai ales cele de la geometrie, nu au fost ușoare. Au putut provoca chiar și pe cei mai buni elevi. 

„Evident că toate problemele pot avea și alte soluții. De multe ori, elevii sunt mai creativi decât no). Subiectul este unul care îi provoacă și pe elevii foarte buni. Calculele, mai ales pe partea de geometrie, nu sunt cele mai simple. Sper că elevii noștri din Sibiu au fost atenți, iar rezultatele obținute de ei vor fi pe măsura efortului depus”, a spus profesorul. 

Rezolvarea subiectelor la matematică

Structura subiectului la matematică a rămas aceeași.

Subiectul I are șase itemi, probleme de algebră tip grilă, cu nivel scăzut de dificultate.

Răspunsurile corecte sunt: 1 – c), 2 – a), 3 – a), 4 – d), 5 – a) și 6 – b).

Rezolvarea lor implică deprinderile de calcul, cu numere naturale, raționale și reale, dar și interpretarea unor date statistice prezentate sub formă de reprezentare grafică cu coloane.

Al doilea subiect este de geometrie. El este structurat tot pe șase itemi tip grilă, cu alegerea răspunsului corect. Rezolvarea lor implică faptul că elevii au cunoștințe elementare pentru calculul segmentelor, unghiurilor, ariei și perimetrului unui pătrat, precum și al ariei laterale a unui con.

Răspunsurile corecte sunt: 1 – d), 2 – d), 3 – b), 4 – c), 5 – c) și 6 – a).

Subiectul al III-lea este alcătuit din șase probleme la care trebuie făcută rezolvarea completă, cu demonstrații.

Prima problemă poate fi rezolvată atât aritmetic, cât și algebric. La subpunctul a), afirmația problemei este falsă: opt pixuri costă cât șase caiete, nu cât cinci caiete. Înlocuind, în informația de la punctul b), pixurile și creioanele în funcție de caiete, se obține prețul unui caiet egal cu șase lei.

La a doua problemă, rezolvarea subpunctului a) (verificarea unei egalități) îi ajută pe elevi să aducă expresia la forma cea mai simplă, obținându-se E(x) = x la puterea a doua + 27 supra x + 3.

​

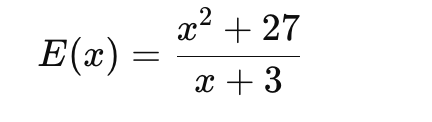
Pentru a demonstra că E(n) este mai mare decât șase, trebuia trecut în partea stângă și se obținea relația (n – 3) la pătrat supra n + 3, mai mare decât 0, care este adevărată, deoarece numărătorul este mai mare decât zero, fiind un pătrat perfect care nu poate fi zero (n ≠ 3), iar numitorul este pozitiv, deoarece este suma dintre un număr natural și 3.

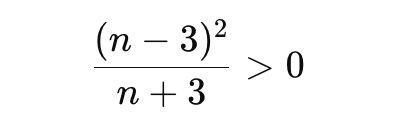
Este posibil ca elevii să aducă la același numitor și să elimine numitorul. În acest caz, este obligatorie observația că n + 3 este pozitiv, lucru pe care, în general, elevii îl omit.

Problema trei este legată de funcții.

Subpunctul a) este foarte simplu (relația dată se verifică ușor).

La subpunctul b), trebuie determinate coordonatele punctului A (2; 0) (intersecția cu axa Ox), ale punctului B (0; –4) (intersecția cu axa Oy) și ale simetricului punctului A față de Oy, punctul C (–2; 0).

Laturile triunghiului ABC se află prin aplicarea formulei specifice (sau a teoremei lui Pitagora) și se obține rezultatul cerut.

Ultimele trei probleme sunt de geometrie plană (problemele 4 și 5) și în spațiu, problema 6.

Subpunctele a) sunt simple și se rezolvă prin aplicarea unor formule.

Pentru rezolvarea subpunctelor b) sunt necesare calcule, nu toate fiind foarte lejere.

La problema 4 b), se cere aflarea unei distanțe. Una dintre idei este calculul ariei triunghiului ADE (care este 36 (radical din 3 – 1)) și apoi al distanței de la punctul D la dreapta AE, care devine înălțime în acest triunghi. Rezultatul final este 3 radical din 2 (radical din 3 – 1).

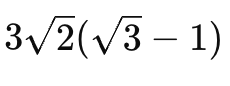
La problema 5 b), se cere calculul ariei unui patrulater convex BPMC, care nu este unul particular, deci nu se află prin aplicarea unei simple formule. Prin scăderea de arii ale unor figuri geometrice pentru care copiii știu formule (trapez dreptunghic / triunghiuri), se obține aria patrulaterului egală cu 36 supra 5.

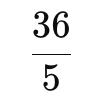
Ultima problemă de geometrie în spațiu cere demonstrarea faptului că dreptele FO și DE sunt perpendiculare. Acest lucru se poate demonstra prin înlocuirea dreptei FO cu dreapta CA, care este paralelă cu ea, și apoi verificarea, prin reciproca teoremei lui Pitagora, că CA și DE sunt perpendiculare. O altă variantă ar fi să demonstreze că dreapta FO este perpendiculară pe planul (DEB), care conține și dreapta DE.

Primele rezultate vor fi afișate pe 3 iulie, iar contestațiile pot fi depuse în perioada 3–5 iulie. Rezultatele finale vor fi publicate pe 10 iulie. 

Citește și: Rezolvarea subiectelor de la Evaluarea Națională de către un profesor de română din Sibiu: „Toate pânzele sus” la primul subiect și compunere la subiectul II

Sursa foto: depositphotos.com/ro

Abonează-te la canalul de WhatsApp al Turnul Sfatului pentru a afla în timp real știrile relevante de la Sibiu: accesează linkul de aici și apasă opțiunea Follow (Urmăriți).

Dacă ți-a plăcut, distribuie articolul și prietenilor tăi